| Математическая запись | a² + b² + c² + ... + n² |
| Сумма квадратов двух чисел | a² + b² |
| Сумма квадратов n чисел | ∑(xᵢ)² где i = 1 до n |
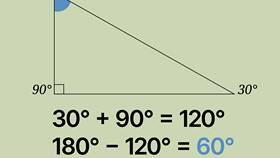
- Представляет квадрат гипотенузы прямоугольного треугольника
- Связана с теоремой Пифагора: c² = a² + b²
- В пространстве - диагональ прямоугольного параллелепипеда
- Квадрат расстояния между точками
- Длина вектора в евклидовом пространстве
- Мера разброса данных в статистике
| Неотрицательность | a² + b² ≥ 0 для любых действительных a, b |
| Равенство нулю | a² + b² = 0 ⇔ a = 0 и b = 0 |
| Формула разложения | (a + b)² = a² + 2ab + b² |
| Два числа | 3² + 4² = 9 + 16 = 25 |
| Три числа | 1² + 2² + 3² = 1 + 4 + 9 = 14 |
| Последовательность | 1² + 3² + 5² = 1 + 9 + 25 = 35 |
Применение в различных областях
- Физика: вычисление энергии, расстояний
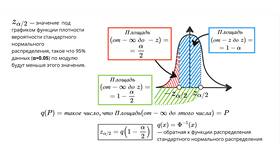
- Статистика: расчет дисперсии и стандартного отклонения
- Машинное обучение: функция потерь в методах оптимизации
- Геометрия: вычисление площадей и объемов
Сумма квадратов представляет собой фундаментальное математическое понятие с многочисленными приложениями. Ее геометрическая интерпретация помогает визуализировать алгебраические свойства, а аналитическая форма широко используется в научных и инженерных расчетах.
