Сумма углов в треугольнике - это фундаментальное свойство евклидовой геометрии, которое изучается в школьном курсе математики. Данное свойство справедливо для любого треугольника независимо от его вида и размеров.
Содержание
Основная теорема о сумме углов
В любом треугольнике сумма внутренних углов равна 180 градусам (или π радиан). Это можно выразить формулой:
| ∠A + ∠B + ∠C | = | 180° |
Доказательство теоремы
Классическое доказательство
- Проведем через вершину B прямую, параллельную стороне AC
- Образовавшиеся углы при точке B будут равны углам A и C как накрест лежащие
- Сумма углов на прямой равна 180°
- Следовательно, ∠A + ∠B + ∠C = 180°
Примеры для разных типов треугольников
| Тип треугольника | Пример углов | Сумма |
| Остроугольный | 60°, 60°, 60° | 180° |
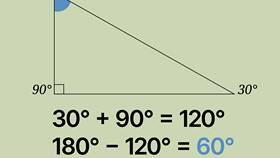
| Прямоугольный | 90°, 45°, 45° | 180° |
| Тупоугольный | 100°, 40°, 40° | 180° |
Практическое применение
- Решение геометрических задач
- Определение неизвестных углов
- Проверка правильности построения треугольников
- Приложения в архитектуре и строительстве
Следствия из теоремы
- В треугольнике не может быть двух прямых или тупых углов
- Внешний угол треугольника равен сумме двух внутренних, не смежных с ним
- Сумма острых углов прямоугольного треугольника равна 90°
Данное свойство треугольников является основой для многих других геометрических теорем и широко применяется в различных областях математики и ее приложениях.